(optional) an application of PAC
We’ll examine an example from the research literature where PAC has been used (and was crucial). After this video, you will understand better which features of hyperfine interaction methods (here PAC) make them sometimes the only tools available to obtain particular information.
In hyperfinecourse A, you learned how the hyperfine level scheme of a nucleus with spin I=5/2 subject to an electric-field gradient looks like :
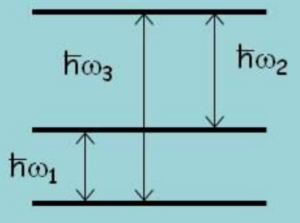
With the knowledge you have, you can even prove that — provided the electric-field gradient has axial symmetry — these relations hold: ω2=2ω1 and ω3=3ω1 (just accept that for know, keep the challenge for proving this for later).
You may take it for granted that the oscillating function in a PAC experiment for this situation will be a superposition of three cosine functions, with these arguments ω1t, ω2t and ω3t. Make a plot of such a superposition (using a spreadsheet or your favourite plotting tool). Make a plot as well for a case where there is no axial symmetry. Make a pdf with both plots, and add a discussion about how you can visually determine from a PAC experiment whether or not an electric field gradient in your sample has axial symmetry.
Upload your pdf via this button:
Quiz Summary
0 of 1 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 1 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 1
1. Question
Although this web site calls this a ‘quiz’, it is not really one. It’s just a way for you to upload your pdf file with answers. If your file would be too large to upload, use this free online tool to compress it (we recommend to do that anyway).
-
Upload your answer to this question.
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
Expected time: 50 minutes (report)
B11-06
